Выбор типа хаос-сигнала
Детерминированный хаос есть решение нелинейного дифференциального уравнения (или их системы), описывающего некоторую автоколебательную систему. На выходе этой системы воспроизводится непериодический процесс (напряжение, ток), по своим статистическим характеристикам близкий к шумовому, который и является решением. В отличие от цифровых схем формирующих ПСП, хаос реализуется аналоговыми методами, однако для повышения стабильности работы СПИ и с целью применения современной цифровой элементной базы при разработке практической системы нам необходимо иметь не непрерывнозначный, а квантованный сигнал с изменением своих мгновенных значений в строго определенные моменты времени, задаваемые генератором тактовых импульсов (ГТИ). Для этого необходимо, чтобы блок вычисления нелинейной функции управлялся в определенные моменты времени, скажем, по фронту прямоугольного импульса, а в цепь ОС в простейшем случае необходимо включить устройство хранения аналогового значения сигнала (рис. 1).
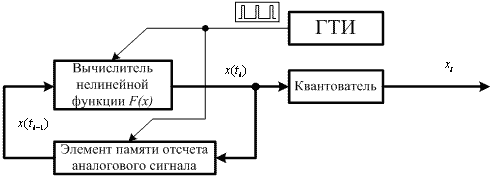
Рис. 1. Структурная схема формирователя дискретного хаос-процесса
На выходе блока вычисления нелинейной функции F(x) действует непрерывнозначный хаос-процесс x(ti) ступенчатого типа, поэтому далее стоит квантователь, от числа уровней квантования которого и зависит вид ШХС на выходе формирователя. Это придает такой схеме гибкость в работе: она способна формировать случайно-подобные последовательности с любой разрядностью, причем непериодического характера. Подобное свойство очень полезно в технике цифровой связи. Определим необходимые параметры функции F(x) и формирователя в целом. Как уже отмечалось, для СПИ первостепенную важность имеет АКФ, а для систем с множественным доступом также ВКФ воспроизводимых на выходе ШХС. Известно, что все известные динамические системы с небольшим числом степеней свободы, обладающие динамическим хаосом: аттрактор Лоренца, аттрактор Ресслера, системы Чуа и т.п. не обладают хорошими корреляционными свойствами Кольцевые системы с запаздыванием и чисто амплитудной нелинейностью также уступают М-последовательностям той же длины. В [5] предлагается формировать ШХС в системах, в которых одновременно присутствует как диссипативная, так и реактивная нелинейность, а также задержка в петле ОС.
Определение структуры формирователя ШХС
ШХС в данной работе предлагается формировать путем манипуляции квадратурных составляющих гармонического несущего колебания парой многоуровневых ортогональных последовательностей (МОП) g1(t) и g2(t) (рис. 2).
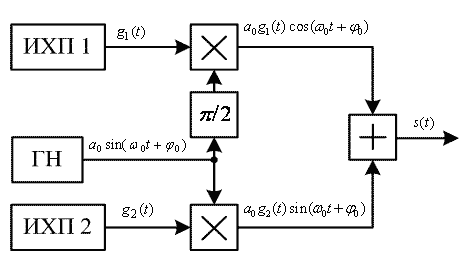
Рис. 2. Формирователь ШХС с квадратурной амплитудно-фазовой манипуляцией
Эти последовательности вырабатываются хаос-генераторами с одинаковой тактовой частотой fT, определяющей длительность элемента τэ каждой из МОП. Для того, чтобы код был сбалансированным на отрезке [0, Т], Т >> τэ, число уровней МОП предполагается четным. Сигнал на выходе формирователя
где a0, ω0, f0 - известные амплитуда, частота и фаза несущего колебания соответственно.
На рис. 3 (а, в) приведены временные диаграммы хаос-последовательностей g1 и g2 соответственно; квадратурных составляющих (б, г) и результирующего сигнала (д).
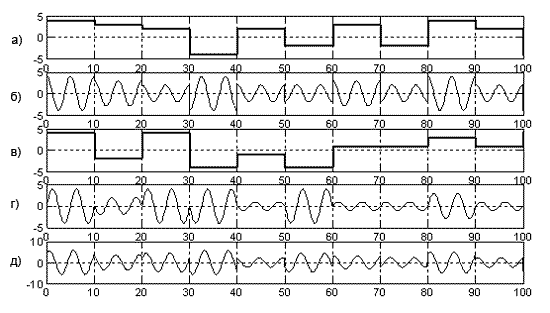
Рис. 3. Временные диаграммы сигнала с квадратурной амплитудно-фазовой манипуляцией
Следует обратить внимание на сложную структуру колебания на выходе формирователя, такой процесс очень схож с узкополосным шумовым процессом, что полезно для СПИ с защитой от обнаружения.
Подобная схема формирования ШХС допускает несколько способов передачи информации. Так как хаос-процессы многоуровневые и для заданной длины кода N имеется значительное количество случайно-подобных последовательностей, то имеется возможность передавать M-ичные символы X(t) путем смены пары МОП {g1i, g2i}, i = 1…M, где {g1i, g2i} и {g1j, g2j} попарно ортогональны. В случае бинарной информационной последовательности со значениями ± 1 возможна передача ортогональными сигналами s1 и s2 путем манипуляции замены g1 на g2 и наоборот, а также инверсная модуляция s1 = - s2. В настоящей работе формирование информационного сигнала происходит с помощью инверсной модуляции. Для двоичной системы структурная схема приемника представлена на рис. 4. Устройство синхронизации сигналов (УСС) формирует опорные сигналы для корреляционных каналов.
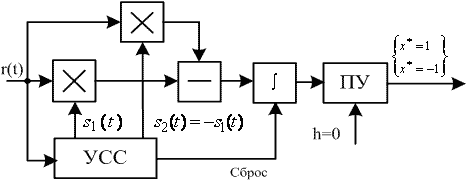
Рис. 4. Структурная схема квазикогерентного различения сигналов
При одинаковых энергиях сигналов порог h в пороговом устройстве (ПУ) равен нулю. Задача синтеза структуры УСС для сигнала вида (1) решается далее.Синтез приемника
Считаем, что на входе УСС действует смесь сигнала и шума.
Случайные процессы τ(t) и f(t) считаем марковскими и определим стохастическими дифференциальными уравнениями
где nτ(t) и nf(t) - независимые белые гауссовские шумы с нулевым математическим ожиданием и спектральными плотностями Nτ/2 и Nf/2 соответственно.
Аддитивный шум y(t) считаем дельта-коррелированным гауссовским процессом со спектральной плотностью N0/2.
Задача синтеза устройства синхронизации состоит в определении уравнений для текущих оценок параметров τ*(t) и f*(t), в построении структурной схемы устройства и в определении дисперсий ошибок синхронизации στ2 и σφ2 в стационарном режиме.
При решении поставленной задачи воспользуемся методами марковской теории нелинейной фильтрации. При этом рассмотрим стационарный режим и гауссовское приближение апостериорной плотности вероятности параметров, при котором апостериорные дисперсии στ2 и σφ2 не зависят от времени:
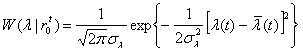 . (5)
. (5)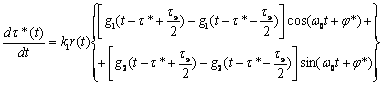 ; (7)
; (7)где ![]() ;
; ![]() .
.
В соответствии с (7) и (8) на рис. 5 представлена схема приемного устройства ШХС, содержащая управляемый генератор несущего колебания (УГ); генераторы хаос-последовательностей g1(t) и g2(t) (ГХП); фазовые дискриминаторы (ФД); синхронные демодуляторы (СД); схему слежения за задержкой (ССЗ), которая обеспечивает подстройку генератора, управляемого напряжением (ГУН). Как и CCЗ схема фазовой автоподстройки частоты (ФАПЧ) состоит из двух колец управления. Управляющее напряжение подается на управляемый генератор после разностного (в CCЗ - суммирующего) устройства.
Схема, представленная на рис. 5, реализует уравнения (7) и (8) и обеспечивает устойчивое слежение за синхропараметрами. За время длительности информационного символа Т синхропараметры не должны сильно изменяться: время их корреляции τкор должно быть много больше Т. Перемножители П1 и П2 с интеграторами обеспечивают выделение на выходе решающего устройства (РУ) информационной последовательности X*(t), которая подается на входной перемножитель.
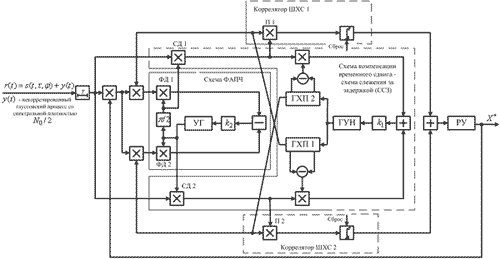
Рис. 5. Приемное устройство ШХС
Моделирование устройства приема и обработки
Модель устройства синхронизации и обработки ШХС с квадратурными компонентами построена согласно синтезированной схеме (рис. 5). Цель моделирования - проверка работоспособности схемы и оценка ее основных качественных показателей и возможности практического применения.
Приведем описание модели (см. рис. 7) и ее краткую характеристику. МОП формируются хаос-генераторами с нелинейностью вида sin x и задержкой в цепи ОС. Ансамбль хаос-сигналов образуется путем изменения начального состояния системы. Число уровней МОП - 8. Информационная манипуляция - по фазе на ± π. Шум в канале - гауссовский. Частота несущей - 2 Гц. Частота смены значений хаос-сигнала - 0,4 Гц. База сигнала B = 10.
Работа схемы на коротких интервалах времени проиллюстрирована в П. 12. На основании наблюдений длительных информационных посылок для ШХС с B = 10 построена зависимость вероятности ошибки Pe от отношения C/Ш (рис. 6).
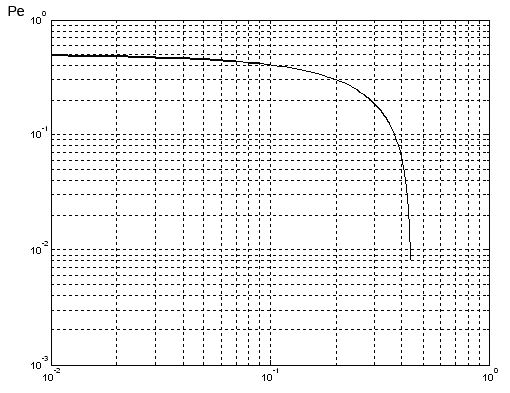
Рис. 6. Зависимость вероятности ошибки при приеме ШХС с квадратурными составляющими от отношения С/Ш
График, изображенный на рисунке, получен аппроксимацией экспериментальных данных с помощью метода полиномиальной регрессии.
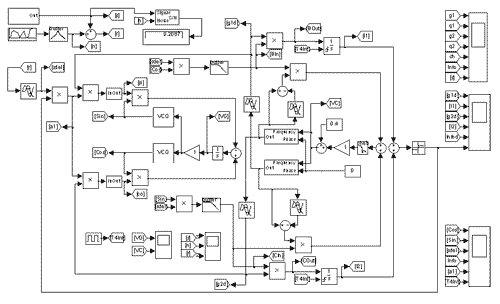
Рис. 7. Модель устройства приема и синхронизации ШХС
Существенно то, что схема обеспечивает устойчивое слежение за синхропараметрами при значительном снижении отношения С/Ш (порядка 0,05). Опираясь на результаты моделирования устройства приема и синхронизации ШХС в различных условиях работы и при различных характеристиках системы в целом, можно сделать следующие выводы:
- схема мало чувствительна к полосе шума - ее увеличение сверх некоторой величины не приводит к заметным ошибкам фильтрации;
- вероятность ошибки на символ Pe мала не только за счет энергетического суммирования элементарных символов, но и по сути сигналов двух квадратурных каналов;
- на практике часто случается, что поражается только одна квадратурная составляющая, вторая же при этом слабо коррелированна с шумом, поэтому на выходе схемы информация оценивается безошибочно, т.е. устойчивость системы при приеме сигналов на фоне помех значительно выше, чем при приеме сигналов с ФМ или ФМн одной гармонической компоненты;
- при значительных ошибках фильтрации параметров начальной фазы и задержки (особенно в начальные моменты вхождения в синхронизм) имеет место явление обратной работы;
- характеристика, изображенная на рис. 6 имеет слабо выраженный пороговый эффект (хорошо видно на графике в линейном масштабе);
- при условии точной синхронизации (установившийся режим слежения) системе присущи достоинства как АМ СПИ - отсутствие порогового эффекта при приеме, - так и ФМ - высокая помехоустойчивость;
- небинарный характер применяемых ШХС несколько ужесточает требования к ДД приемного устройства;
- исследования проводились с заведомой расстройкой по частоте и задержке при q = 0,3, в результате показано, что уверенный захват частоты сигнала и слежение за его фазой происходили при расстройке ± 5 % от истинного значения частоты опорного колебания за время равное 120*1/f0; стационарный режим слежения по задержке устанавливался приблизительно за то же время при начальной задержке в пределах апертуры дискриминационной характеристики ССЗ равной длительности элементарного символа.
Список источников см. здесь.
Автор:dvv
Дубровский Василий
г. Минск, Беларусь

