В последнее время в России широкое распространение получили цифровые запоминающие осциллографы (ЦЗО) реального времени. Причем, речь идет не о простейших приборах такого класса, к которым можно причислить даже звуковые карты компьютеров, а об осциллографах «high-end» класса от мировых лидеров, таких, как Tektronix, LeCroy и Agilent Technologies. Эти средства измерения обладают характеристиками, еще вчера казавшимися недостижимыми для осциллографов реального времени. В совокупности с удобством их использования это позволяет говорить об их неоспоримых преимуществах по сравнению с аналоговыми высокочастотными осциллографами. Однако, те же преимущества цифровой техники, которые помогают добиться такого превосходства, вызывают у некоторых потребителей чувство недоверия в полученных результатах.
В первую очередь такая реакция связана с широким применением программных методов обработки цифровых сигналов в ЦЗО. Более того, мировые лидеры в производстве осциллографов все больше переносят фронт конкурентной борьбы с участка «железа» на участок программных средств обработки данных. Тесты, предлагаемые для сравнения осцилллографов-конкурентов, проверяют именно возможности программного обеспечения (хотя косвенная оценка аналоговой части также присутствует). Но даже специалисты ведущих научных журналов не всегда могут объяснить полученные результаты [1].
Что уж говорить о неподготовленных пользователях, которые, видя первоначально на экране осциллографа «непонятную» картинку, превращающуюся после программной обработки в идеальную синусоиду, подозревают прибор в некоем шаманстве. Соответственно, пользователи не понимают: показывает их средство измерения реальные характеристики сигнала или то, что прибор позволяет им увидеть? Попробуем развеять некоторые предубеждения в отношении пост-математической обработки данных в ЦЗО. Видов такой обработки существует множество, выделим из них те, которые в наибольшей степени влияют на метрологические характеристики прибора и на форму отображаемых на экране сигналов. К таким алгоритмам обработки, прежде всего, относятся [2]:
• реконструкция (интерполяция) сигнала по ограниченному числу отсчетов;
• выравнивание амплитудно-частотной характеристики (АЧХ) осциллографа;
• коррекция фазо-частотной характеристики осциллографа;
• фильтрация собственных шумов осциллографа;
• программное расширение полосы пропусканияосциллографа.
Остановимся подробнее на алгоритмах интерполяции типа «sin x/x», которые предоставляют наиболее зримый эффект и применение которых обусловлено прежде всего конечной частотой дискретизации аналогово-цифровых преобразователей ЦЗО. Для примера возьмем осциллограф LeCroy 7100, обладающий расширенными возможностями по выбору частот дискретизации. Подадим на его вход синусоидальный сигнал с частотой 1 МГц при частоте дискретизации прибора 5 МГц. Таким образом, на один период сигнала приходится 5 отсчетов, что не формирует на экране осциллограмму в виде синуса (рис. 1). Зато после включения интерполяции на экране наблюдается «идеальный» синус (рис. 2). Однако есть и другой вариант, когда интерполятор прилежно пытается сделать такой же «идеальный» синус из поступающего на вход прямоугольного сигнала частотой 1 МГц (рис. 3 и 4). Далее рассмотрим предпосылки, которые лежат в основе алгоритма интерполяции sin x/x, и ограничения на ее применение.
В настоящее время в ЦЗО применяют два вида алгоритмов интерполяции: линейный и sin x/x. Линейная интерполяция осуществляется в предположении, что отсчеты аналогово-цифрового преобразователя (АЦП) ЦЗО соединяет прямая линия. Это очень простое и малоправдоподобное предположение, которое дает ограниченные результаты. Поэтому все чаще в ЦЗО применяют интерполяцию sin x/x. Здесь следует подчеркнуть два важных момента:
1) любая интерполяция основана на наборе данных из АЦП осциллографа, поэтому даже если в приборе нет соответствующего алгоритма, пользователь может создать его сам в любом прикладном пакете;
2) применение интерполяции sin x/x имеет свои ограничения, при их нарушении могут серьезно исказиться результаты измерений.
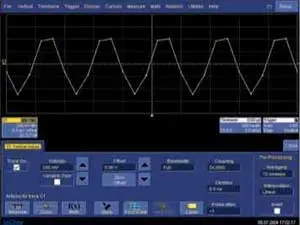
Рис. 1. Интерполяция линейная, частота дискретизации — 5 МГц, входной сигнал — синус с частотой 1 МГц
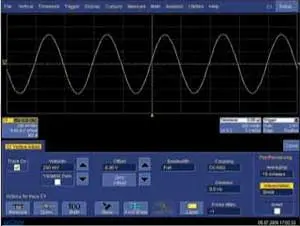
Рис. 2. Интерполяция sin x/x, частота дискретизации — 5 МГц, входной сигнал — синус с частотой 1 МГц
Итак, что же скрывается за фразой «интерполяция sin x/x»? При ближайшем рассмотрении оказывается, ничего загадочного в данном алгоритме нет. На самом деле это реализация положений всем известной теоремы Котельникова-Найквиста [3] о том, что любая непрерывная функция, спектр которой ограничен частотой Fmax, полностью определяется своими отсчетами через интервал времени не более ?t=1/2Fmax. Сигнал восстанавливается по формуле:
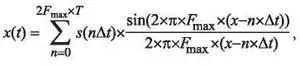
где s — дискретные отсчеты функции x(t), Т— интервал времени, для которого проводится реконструкция. Данная формула является основой алгоритма интерполяции sin x/x.
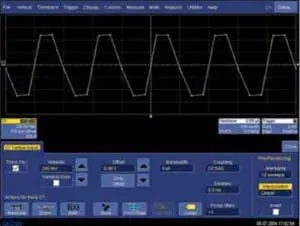
Рис. 3. Интерполяция линейная, частота дискретизации — 5 МГц, входной сигнал — меандр с частотой 1 МГц
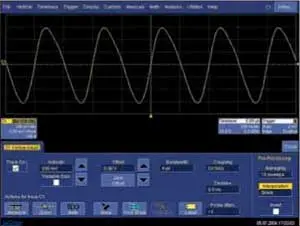
Рис. 4. Интерполяция sin x/x, частота дискретизации — 5 МГц, входной сигнал — меандр с частотой 1 МГц
Таким образом, реализация данного давно известного алгоритма в ЦЗО не является каким-то «ноу-хау» отдельных фирм-производителей. Конечно, способы реализации интерполяции могут быть разными, в том числе и по скорости получения результата, но основа одна — теорема Котельникова. Так что при желании можно провести интерполяцию полученных данных в пакете MathCad (рис. 5) или любом другом.
Теперь остановимся на ограничениях в применении теоремы Котельникова и ее реализации в ЦЗО. Ограничение только одно — спектр сигнала, поступающего на оцифровку, не должен иметь в своем составе частот со сколь-нибудь значимой амплитудой, превышающих Fmax. Для соблюдения этих условий аналоговая полоса пропускания должна иметь вид идеального фильтра нижних частот с граничной частотой, меньшей половины частоты дискретизации (частота Найквиста). Тогда, даже если в спектре сигнала есть составляющие, превышающие частоту Найквиста, то они будут подавляться аналоговой частью осциллографа. Реальные осциллографы имеют другие виды АЧХ. Наиболее распространенными для аналоговых осциллографов являются АЧХ, описываемые фильтром Гаусса. К сожалению, АЧХ таких фильтров имеют плавный спад, поэтому в ЦЗО реализуют АЧХ, описываемые фильтрами высших порядков и имеющие достаточно резкий спад (рис. 6).
Какие же недостатки у интерполяции sin x/x? Если спектр сигнала ограничен частотой меньшей, чем частота Найквиста, то недостатков практически нет. К таковым можно отнести потери времени, затрачиваемые на интерполяцию. Но при наличии в осциллографах мощных процессоров эти потери пренебрежимо малы, тем более по сравнению со временем простоя ЦЗО. Если же в спектре импульсного сигнала есть высокочастотные компоненты, то при применении алгоритма sin x/x возможно появление программно наведенных выбросов на вершине импульса и в паузах (рис. 7, феномен Гиббса) [4]. Однако программные ошибки будут намного меньше, чем аппаратные ошибки, связанные с тем, что высокочастотные компоненты лежат вне аналоговой полосы пропускания ЦЗО.
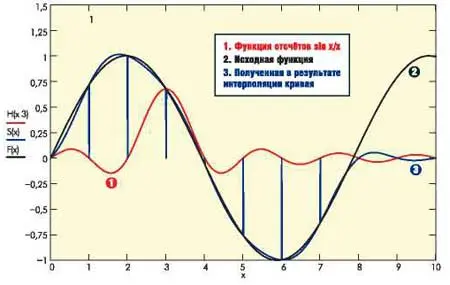
Рис. 5. Интерполяция sin x/x в пакете MathCad
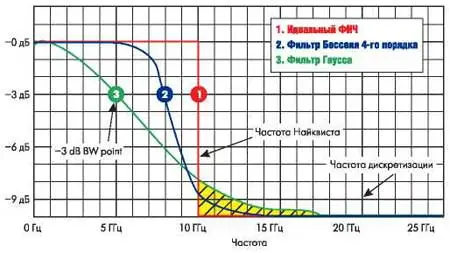
Рис. 6. Фильтры нижних частот, описывающие АЧХ осциллографа
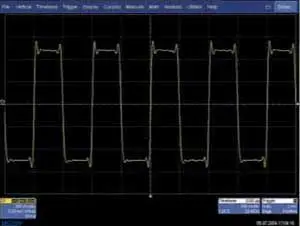
Рис. 7. Интерполяция sin x/x, частота дискретизации — 25 МГц, входной сигнал — меандр с частотой 1 МГц
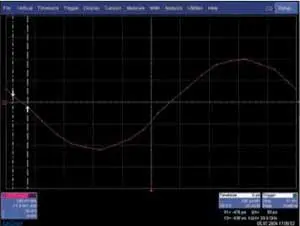
Рис. 8. Интерполяция линейная, частота дискретизации — 20 ГГц, входной сигнал — синус с частотой 1 ГГц
К достоинствам интерполяции sin x/x следует отнести значительное улучшение точности и разрешения при измерениях временных интервалов в реальном времени. Если максимальная частота дискретизации для ЦЗО на сегодня составляет 20 ГГц (дискретность по времени между отсчетами составляет 50 пс, рис. 8), то при интерполяции sin x/x вычисляется дополнительно от 8 до 16 точек. В приборах фирмы LeCroy дополнительное вычисление 9 точек уменьшает интервал дискретизации до 5 пс (рис. 9), то есть на порядок [5]. Таким образом, при правильном использовании преимущества от применения алгоритма sin x/x значительно перекрывают все возможные недостатки.
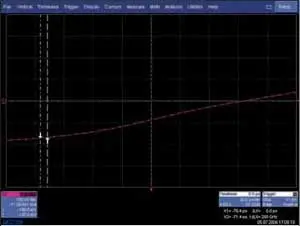
Рис. 9. Интерполяция sin x/x, частота дискретизации — 20 ГГц, входной сигнал — синус с частотой 1 ГГц
Тем не менее, во всех осциллографах мировых лидеров данный вид интерполяции при желании можно отключить. При этом максимальную гибкость реализует фирма LeCroy, в осциллографах которой этот алгоритм выключен по умолчанию, и пользователю предоставляется право самому включать данный режим и оценивать корректность его применения.
В заключение приведем простой экспериментальный способ проверки правильности работы алгоритма sin x/x. На ЦЗО необходимо подать периодическую последовательность импульсов с крутым фронтом и определить переходную характеристику осциллографа в режиме эквивалентной дискретизации и в режиме реального времени с включенной интерполяцией sin x/x.
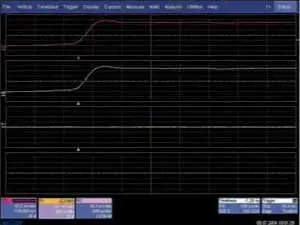
Рис. 10. Канал С2: переходная характеристика осциллографа при эквивалентной частоте дискретизации 100 ГГц; канал М2: переходная характеристика осциллографа в реальном времени при частоте дискретизации 20 ГГц и интерполяции sin x/x; канал F1: разность осциллограмм по С2 и М2
При корректной работе алгоритма отличийбыть не должно (рис. 10).
Литература
1. Dan Strassberg // EDN. 2003. February 6.
2. Application Notes 1494. Agilent Technologies.
3. Гоноровский И. С. Радиотехнические цепи и сигналы // М.: Радио и связь. 1986.
4. John Pickerd. DSP in High Perfomance Oscilloscopes // White Paper. Tektronix Inc.
5. Application Brief WM441. LeСroy.
Автор: Алексей Пивак
